2023年成考高起点每日一练《数学(理)》1月30日专为备考2023年数学(理)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、过点(0，1)且与直线x+y+1=0垂直的直线方程为( )

• A：y=x+1
• B：y=2x+1
• C：y=x
• D：y=x-1

答 案：A

解 析：与直线x+y+1=0垂直的斜率是1,并且该直线同时过点(0,1)，所以该直线的方程应该为y-1=1*(x-0)，即y=x+1,答案为：A

2、曲线y=5/x-2-2的对称中心为（）。

• A：(1,4)
• B：(2,-2)
• C：(2,1)
• D：(4,1)

答 案：B

解 析：将y=5/x向右平移两个单位，向下平移两个单位得原函数，因此图像关于(2,-2)对称。

3、已知圆x2＋y2＋4x－8y＋11＝0，经过点P（1，0）作该圆的切线，切点为Q，则线段PQ的长为（　　）

• A：10
• B：4
• C：16
• D：8

答 案：B

解 析：x2＋y2＋4x－8y＋11＝0（x＋2）2＋（y－4）2＝9．则P点距圆心的长度为

4、右图是二次函数 的部分图像，则（）。

• A：b > 0，c > 0
• B：b > 0，c < 0
• C：b<0，c>0
• D：b<0，c<0

答 案：A

解 析：该小题主要考查的知识点为二次函数图像. 【考试指导】由图像可知，当x = 0时：y = c>0,也就是图像与y轴的交点；图像的对称轴1=-b/2< 0,则b> 0.

主观题

1、

答 案：

2、

答 案：

3、设函数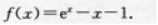
(I)求f(χ)的单调区间；
(Ⅱ)求f(χ)的极值。

答 案：

4、已知△ABC中，A=30°，AC=BC=1.求(Ⅰ)AB；(Ⅱ)△ABC的面积.

答 案：(Ⅰ)由已知得C=120° 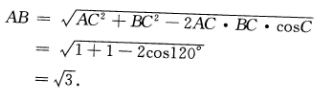(Ⅱ)设CD为AB边上的高，那么 CD=AC·sin30°=1/2 △ABC的面积为

填空题

1、过点A(2,4)并且与直线2x-3y+1=0平行的直线方程为（）。

答 案：2x-3y+8=0

解 析：设直线方程为2x-3y+D=0，将A(2,4)代入得D=8，所以直线方程为2x-3y+8=0。

2、已知数列{a_n}的前n项和S_n=2n+1，则a₂=（）。

答 案：2

解 析：a₁=S₁=2+1=3，故a₂=S₂一S₁=2×2+1—3=2。