2022年成考高起点每日一练《数学(理)》10月26日专为备考2022年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、直线3x+y-2=0经过( )
- A:第一、二、四象限
- B:第一、二、三象限
- C:第二、三、四象限
- D:第一、三、四象限
答 案:A
解 析:直线3z+y-2=0可整理为y=-3x+2,由此可以看出直线过(0,2)点,且直线的斜率为-3,故直线过第一、二、四象限
2、已知双曲线 的离心率为3,则m=()
的离心率为3,则m=()
- A:4
- B:1
- C:

- D:2
答 案:C
解 析:由题知,a2=m,b2=4,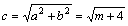 ,其离心率
,其离心率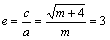 ,故
,故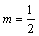 .
.
3、若a,b,c为实数,且a≠0.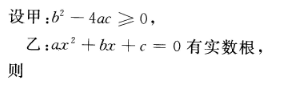 ()。
()。
- A:甲既不是乙的充分条件,也不是乙的必要条件
- B:甲是乙的必要条件,但不是乙的充分条件
- C:甲是乙的充分必要条件
- D:甲是乙的充分条件,但不是乙的必要条件
答 案:C
解 析:该小题主要考查的知识点为简易逻辑.【考试指导】
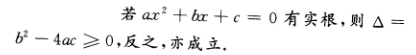
4、过点(0,1)且与直线x+y+1=0垂直的直线方程为( )
- A:y=x+1
- B:y=2x+1
- C:y=x
- D:y=x-1
答 案:A
解 析:与直线x+y+1=0垂直的斜率是1,并且该直线同时过点(0,1),所以该直线的方程应该为y-1=1*(x-0),即y=x+1,答案为:A
主观题
1、等差数列{an}中,a1=-393,a2+a3=-768,{bn}是等比数列,q∈(0,1),b1=2,{bn}的前n项和为20,求:(Ⅰ)求an,bn;
(Ⅱ)解不等式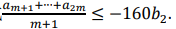
答 案: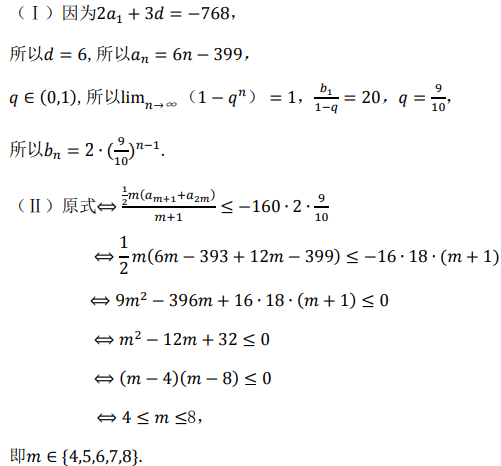
2、建筑一个容积为8000m3,深为6m的长方体蓄水池,池壁每m2的造价为15元,池底每m2的造价为30元。(Ⅰ)把总造价y(元)表示为长x(m)的函数;
(Ⅱ)求函数的定义域。
答 案:
3、已知{an}为等差数列,且a3=a5+1. (Ⅰ)求{an}的公差d; (Ⅱ)若a1=2,求{an}的前20项和S20.
答 案:(Ⅰ)设公差为d,知a5=a+32d,
故a5=a3+2d=a3-1,
因此有d=-1/2.
(Ⅱ)由前n项和公式可得
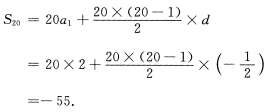
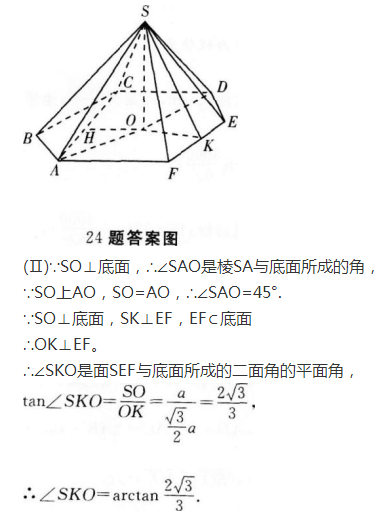
4、
答 案:
填空题
1、从某公司生产的安全带中随机抽取10条进行断力测试,测试结果(单位:kg)如下:3722、3872、4004、4012、3972、3778、4022、4006、3986、4026则该样本的样本方差为______ (精确到0.1).
答 案:10928.8
解 析:该小题主要考查的知识点为方差.

2、方程Ax2+Ay2+Dx+Ey+F=0(A≠0)满足条件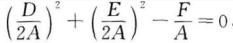 ,它的图像是()。
,它的图像是()。
答 案: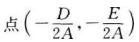
精彩评论