2022年成考高起点每日一练《数学(文史)》5月17日专为备考2022年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、双曲线3x2﹣4y2=12的焦距为()。
- A:
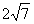
- B:
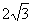
- C:4
- D:2
答 案:A
解 析:本题考查了双曲线的焦距的知识点。
3x2-4y2=12可化为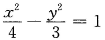 ,即a2=4,b2=3,则
,即a2=4,b2=3,则 则焦距
则焦距 。
。
2、已知圆22+y2+4x-8y+11=0,经过点P(1,o)作该圆的切线,切点为Q,则线段PQ的长为 ( )
- A:10
- B:4
- C:16
- D:8
答 案:B
解 析:本题主要考查的知识点为圆的切线性质和线段的长度.【应试指导】

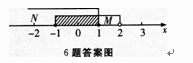
3、
- A:

- B:

- C:

- D:
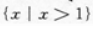
答 案:A
解 析:本题主要考查的知识点为集合之间的关系. 【应试指导】用数轴表示(如图).
4、某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共有 ( )
- A:7种
- B:4种
- C:5种
- D:6种
答 案:C
主观题
1、设函数f(x)=x3-3x2-9x.求 (I)函数f(x)的导数;(II)函数f(x)在区间[1,4]的最大值与最小值.
答 案:
2、已知等差数列{an}的首项与公差相等,{an}的前n项的和记作Sn,且S20=840.(I)求数列{an}的首项a1及通项公式;(Ⅱ)数列{an}的前多少项的和等于847.
答 案:
3、已知数列{an}的前n项和Sn=n2-2n.求(I){an}的前三项;(II){an}的通项公式.
答 案:
4、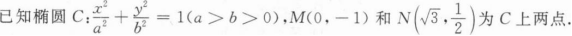
(Ⅰ)求C的标准方程;
(Ⅱ)求C的左焦点到直线MN的距离
答 案:(Ⅰ)
(Ⅱ)
填空题
1、已知函数f(x)=2x+1,则f(2x)=()。
答 案:4x+1
解 析:f(2x)=2×2x+1=4x+1
2、圆x2+y2=25的圆心到直线x+y+1=0的距离为_______
答 案: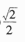
精彩评论