2023年成考高起点每日一练《数学(文史)》9月26日专为备考2023年数学(文史)考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、已知向量i,j为互相垂直的单位向量，向量a=2i+mj，若|a|=2，则m=（）

• A：-2
• B：-1
• C：0
• D：1

答 案：C

解 析：由题可知a=(2,m),因此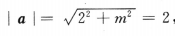，故m=0.

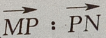2、已知点M(-2,5),N(4,2),点P在上，且=1:2，则点P的坐标为（）

• A：
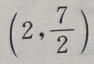
• B：(0,4)
• C：(8,2)
• D：(2,1)

答 案：B

解 析：由题意得：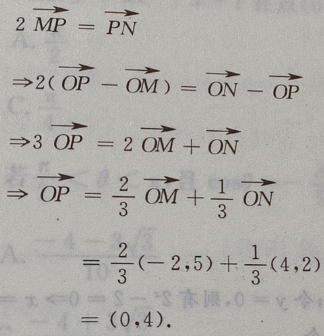  

3、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

4、函数的图像与直线y=4的交点坐标为（）

• A：(0,4)
• B：(4,64)
• C：(1,4)
• D：(4,16)

答 案：C

解 析：令y=4^x=4，解得x=1，故所求交点为（1,4).

主观题

1、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．

答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积

2、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图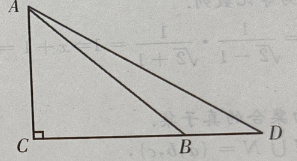  

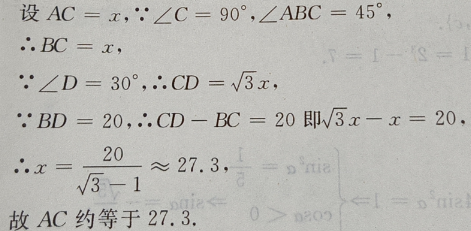
3、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

4、设函数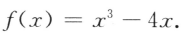
(I）求f'(2)；
(II）求f(x）在区间[一1,2]的最大值与最小值．

答 案：(I）因为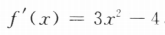，所以f'(2)=3×2²-4=8.(II）因为x＜-1，f(-1)=3.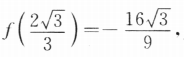f(2)=0.
所以f(x）在区间[一1,2]的最大值为3，最小值为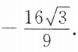

填空题

1、函数f(x)=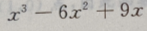在区间[-3,3]上的最大值为（）  

答 案：4

解 析：这题考的是高次函数的最值问题，可用导数来求函数在区间[-3,3]上的最值。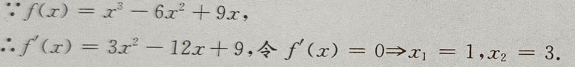 列出表格 由上表可知函数在[-3,3]上，在x=1点处有最大值为4.  

2、已知向量a=(3,2),b=(-4,x),且a⊥b，则x=（）  

答 案：6

解 析：∵a⊥b， ∴3×(-4)+2x=0 ∴x=6.