2023年成考高起点每日一练《数学(文史)》9月2日专为备考2023年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、点(2,4)关于直线y=x的对称点的坐标为()
- A:(4,2)
- B:(-2,-4)
- C:(-2,4)
- D:(-4,-2)
答 案:A
解 析:点(2,4) 关于直线y=x对称的点为(4,2)
2、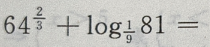 ()
()
- A:8
- B:14
- C:12
- D:10
答 案:B
解 析: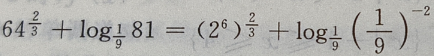
3、若函数f(x)=1+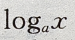 在(0,+∞)上是减函数,则()
在(0,+∞)上是减函数,则()
- A:a>1
- B:a>2
- C:1
- D:0
- D:0
答 案:D
解 析:由已知条件函数f(x)=1+ 4、已知向量i,j为互相垂直的单位向量,向量a=2i+mj,若|a|=2,则m=() 答 案:C 解 析:由题可知a=(2,m),因此 主观题 1、设函数 答 案:(I)因为 2、设椭圆的中心是坐标原点,长轴在x轴上,离心率 答 案:由题意,设椭圆方程为 3、设函数f(x) 答 案:(Ⅰ)由已知得f'= 4、如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)
答 案:如图 填空题 1、 答 案:3 解 析: 2、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: 解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=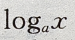 在(0,+∞)上是减函数,及对数函数
在(0,+∞)上是减函数,及对数函数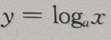 的性质可得底数0
的性质可得底数0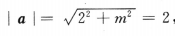 ,故m=0.
,故m=0.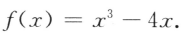
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.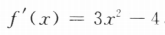 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.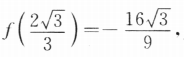 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为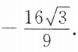
 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
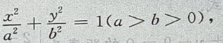 由
由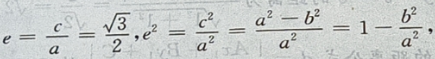
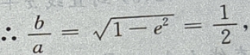 设P
设P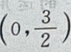 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
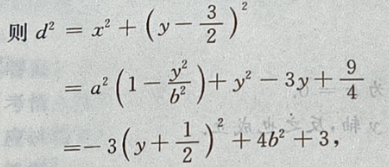
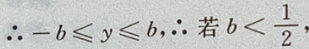 则在y=-b时,
则在y=-b时,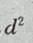 最大,即d也最大。
最大,即d也最大。
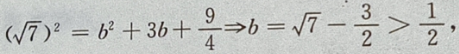

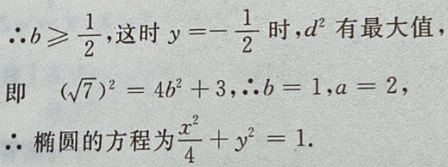
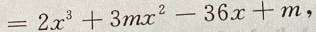 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间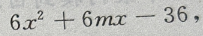 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=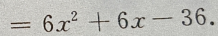 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-3
当x<-3时,f'(x)>0;
当-3
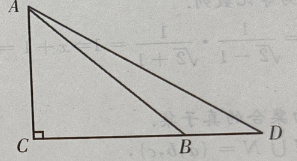
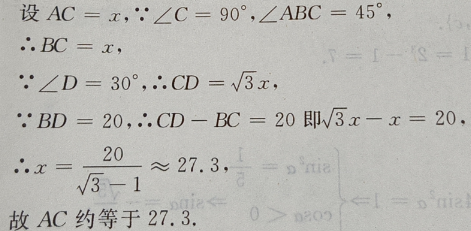
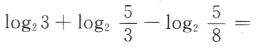 ()
()
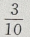
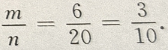
精彩评论