2023年成考专升本每日一练《高等数学一》10月21日专为备考2023年高等数学一考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、函数y=f(x)在点x0处可导的充分必要条件是()。
- A:它在该点处的左导数和右导数存在
- B:它在该点处连续
- C:它在该点处存在极限
- D:它在该点处可微
答 案:D
解 析:D项,对于一元函数来说,函数在某一点可导和在某一点可微等价.A项,函数在某一点的左导数和右导数存在且相等是函数在该点可导的充分必要条件.B项,可导一定连续,但连续不一定可导,例如函数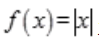 在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
2、设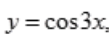 则y'=()。
则y'=()。
- A:
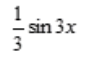
- B:
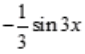
- C:
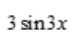
- D:
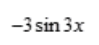
答 案:D
解 析: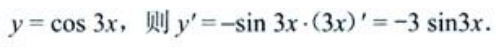
3、设y=x+lnx,dy=()。
- A:
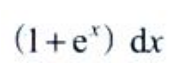
- B:
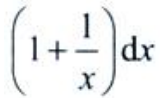
- C:
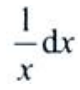
- D:
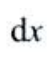
答 案:B
解 析:y=x+lnx,则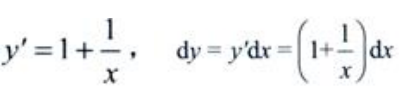 。
。
主观题
1、求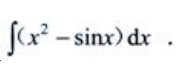
答 案:解: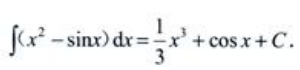
2、求过两点M1(1,-1,-2),M2(-1,1,1)作平面,使其与y轴平行的平面方程。
答 案:解:所求平面法向量同时垂直y轴及向量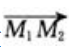 ,即
,即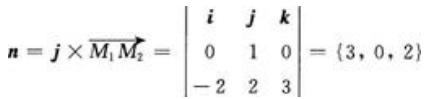 由点法式可得所求平面为3x+2z+1=0。
由点法式可得所求平面为3x+2z+1=0。
3、求微分方程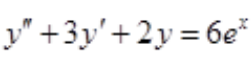 的通解.
的通解.
答 案:解:原方程对应的齐次方程为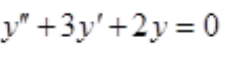 。特征方程为,r2+3r+2=0,特征值为r1=-2,r2=-1。齐次方程的通解为y=C1e-2x+C2e-x。
。特征方程为,r2+3r+2=0,特征值为r1=-2,r2=-1。齐次方程的通解为y=C1e-2x+C2e-x。
设特解为y*=Aex,代入原方程有6A=6,得A=1。
所以原方程的通解为y=C1e-2x+C2e-X+ex(C1,C2为任意常数)。
填空题
1、微分方程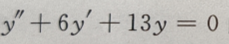 的通解为()
的通解为()
答 案: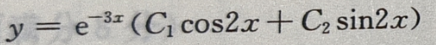
解 析:微分方程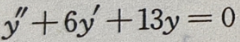 的特征方程为
的特征方程为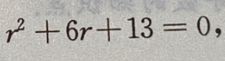 特征根为
特征根为 所以微分方程的通解为
所以微分方程的通解为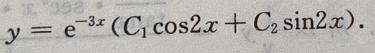
2、设二元函数z=eusinv,u=xy,v=x-y,则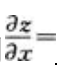 ()。
()。
答 案:
解 析: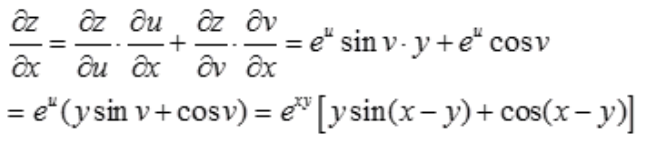
3、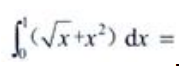 ()。
()。
答 案:1
解 析: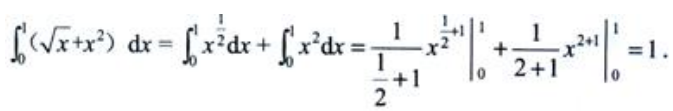
简答题
1、设函数z(x,y)由方程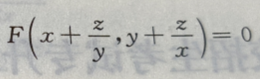 所确定
证明:
所确定
证明: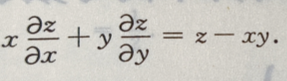
答 案: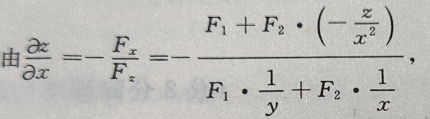
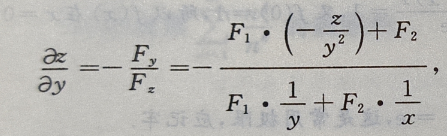 所以
所以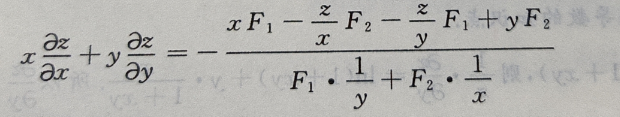
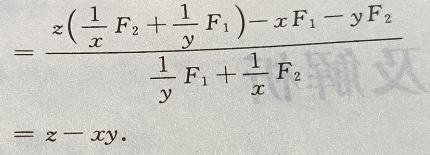
精彩评论