2023年成考专升本每日一练《高等数学一》10月20日专为备考2023年高等数学一考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

单选题

1、当x→0时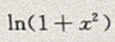，为x的（）  

• A：高阶无穷小量
• B：等价无穷小量
• C：同阶但不等价无穷小量
• D：低阶无穷小量

答 案：A

解 析：由题可知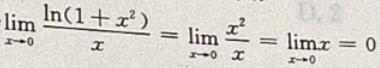，故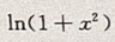是x的高阶无穷小量。

2、若级数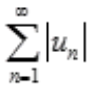收敛，则（）。

• A：发散
• B：条件收敛
• C：绝对收敛
• D：无法判定敛散性

答 案：C

解 析：级数绝对收敛的性质可知，收敛，则收敛，且为绝对收敛。

3、设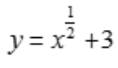，则（）。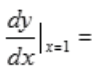

• A：2
• B：
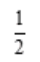
• C：－2
• D：

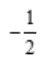
答 案：B

解 析：,。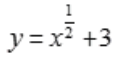

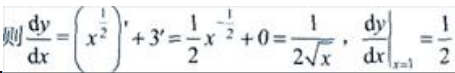主观题

1、设z＝f（x，y）是由方程所确定，求。

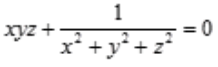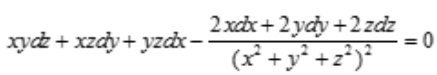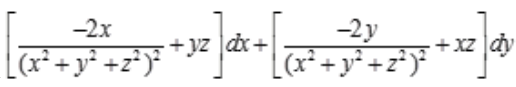
答 案：解：由得全微分方程：化简得所以。

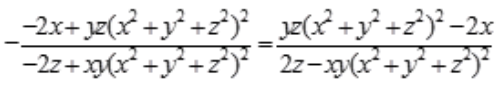2、设z＝（x，y）由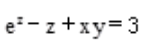所确定，求dz。

答 案：解：设F（x，y，z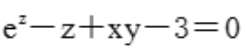）＝，则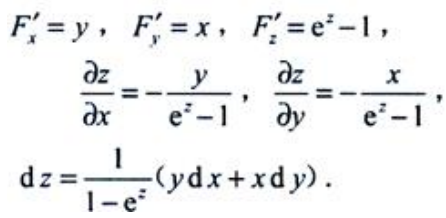

3、设y＝（sinx）e^x＋2，求y'。

答 案：解：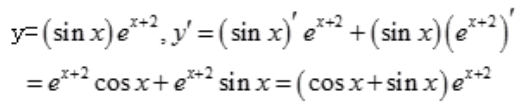

填空题

1、＝（）。

答 案：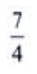

解 析：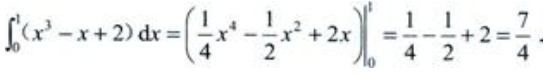

2、设函数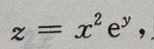则全微分dz=（）

答 案：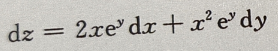

解 析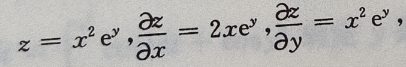：则

3、过原点且垂直于y轴的平面方程为（）。

答 案：y＝0

解 析：过原点且垂直于y轴的平面即x轴所在的平面，方程为y＝0。

简答题

1、讨论级数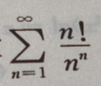敛散性。

答 案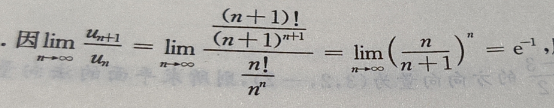：所以级数收敛。