2023年成考专升本每日一练《高等数学二》10月17日专为备考2023年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、函数f(x)的导函数f(x)的图像如下图所示，则在（－∞，＋∞）内f(x)的单调递增区间是（）.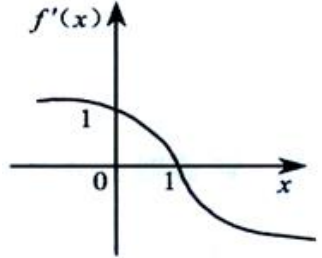

• A：（－∞，0）
• B：（－∞，1）
• C：（0，＋∞）
• D：（1，＋∞）

答 案：B

解 析：因为x在（－∞，1）上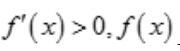，单调增加.

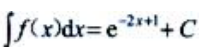2、设，则（）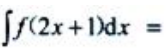

• A：
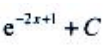
• B：
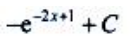
• C：
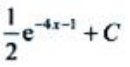
• D：

答 案：C

解 析：由题意得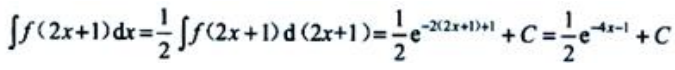

主观题

1、某班有党员10人，其中女党员有6人，现选3人组成党支部．设事件A＝{党支部中至少有1名男党员}，求P（A）．

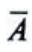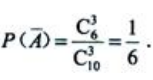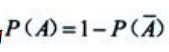答 案：解：＝{党支部中没有男党员}，则因为，所以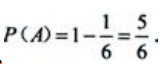

2、某射手击中10环的概率为0.26，击中9环的概率为0.32，击中8环的概率为0.36，求在一次射击中不低于8环的概率．

答 案：解：设A＝{击中10环），B＝{击中9环），C＝{击中8环），D＝{击中不低于8环），则D＝A＋B＋C，由于A，B，C相互独立，所以P（D）＝P（A＋B＋C）＝P（A）＋P（B）＋P（C）＝0.26＋0.32＋0.36＝0.94

填空题

1、设函数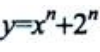，则＝（）．

答 案：n!

解 析：先求出函数的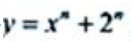的n阶导数，再将x＝1代入，注意：2ⁿ是常数项．因为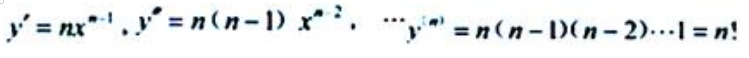所以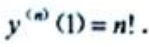

2、设曲线在点M处切线的斜率为2，则点M的坐标为（）  

答 案：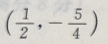

解 析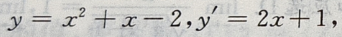：由导数的几何意义可知，若点M的坐标为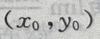则解得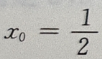

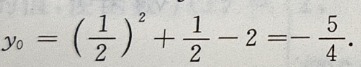
简答题

1、求函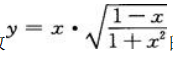数的倒数。  

答 案：等式两边同时取对数得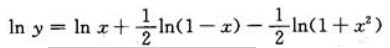 方程两边同时对x求导有 故

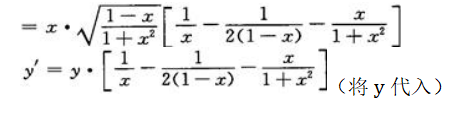
2、求曲线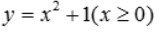与y＝x＋1所围成的图形分别绕x轴和y轴旋转所得旋转体的体积．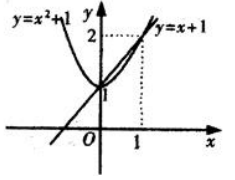

答 案：（1）绕x轴旋转的体积为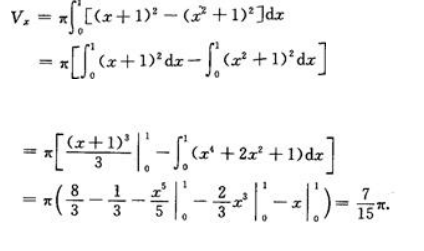 （2）绕y轴旋转的体积为