2023年成考专升本每日一练《高等数学二》10月14日专为备考2023年高等数学二考生准备，帮助考生通过每日坚持练习，逐步提升考试成绩。

判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、（）.

• A：0
• B：
• C：1
• D：e

答 案：B

解 析：因为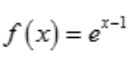是初等函数，在定义区间（x∈R）内是连续的，其极限值等于函数值，所以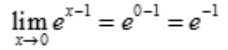

2、设函数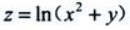则（）  

• A：
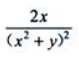
• B：
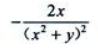
• C：
• D：

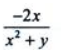
答 案：B

解 析：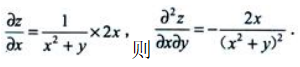

主观题

1、设生产某种产品的数量z与所用两种原料A的数量x吨和B的数量y吨间有关系式z＝z（x，y）＝xy，欲用100万元购买原料，已知A，B原料的单价分别为每吨1万元和每吨2万元，问购进两种原料各多少时，可使生产的产品数量最多？

答 案：解：当购进A原料x吨时，需花费x万元，此时，还可购进B原料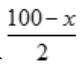吨，函数z＝xy变为关于x的一元函数，，其定义域为[0，100]．求出z'＝－x＋50，令z'＝0，即－x＋50＝0，解得x＝50．当x＜50时,z'＞0；当x＞50时,z'＜0．所以x＝50是函数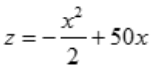的极大值点，显然也是最大值点．
此时，y＝25，即当购进A原料50吨．Ｂ原料25吨时，生产的产品数量最多．

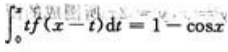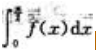2、已知函数f（x）连续，，求的值．

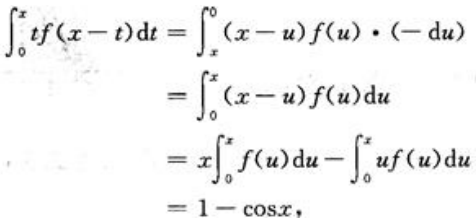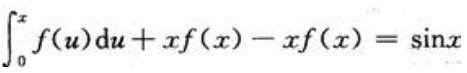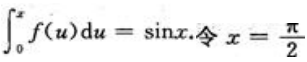答 案：解：令x－t＝u，有-dt＝du．当t＝0时，u＝x；当t＝x时，u＝0．两边对x求导，得即，得．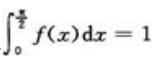

填空题

1、曲线f(x)=xInx-x在x＝e处的法线方程为()

答 案：y+x-e＝0

解 析：因为 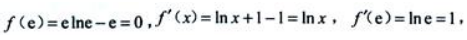故所求法线方程为 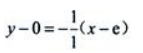即y+x-e＝0.

2、设=（）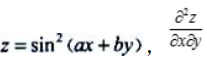  

答 案：2abcos2（ax＋by）  

解 析：

简答题

1、求极限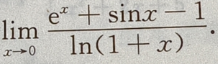  

答 案：原式=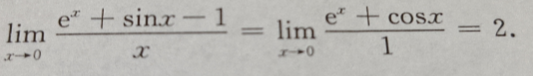

2、计算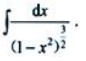  

答 案：设x＝sint，dx＝costdt， 所以