2023年成考专升本每日一练《高等数学二》10月6日专为备考2023年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、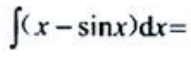 ().
().
- A:x2+cosx+C
- B:
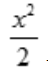 +cosx+C
+cosx+C - C:x2-sinx+C
- D:
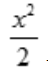 -sinx+C
-sinx+C
答 案:B
解 析: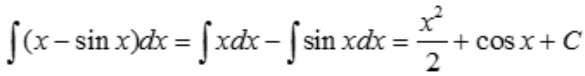 .
.
2、函数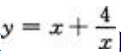 的单调减少区间为().
的单调减少区间为().
- A:(-∞,-2)和(-2,+∞)
- B:(-2,2)
- C:(-∞,0)和(0,+∞)
- D:(-2,0)和(0,2)
答 案:D
解 析:由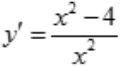 ,令y'=0得驻点为(2,±2),而不可导点为x=0.列表讨论如下:
,令y'=0得驻点为(2,±2),而不可导点为x=0.列表讨论如下: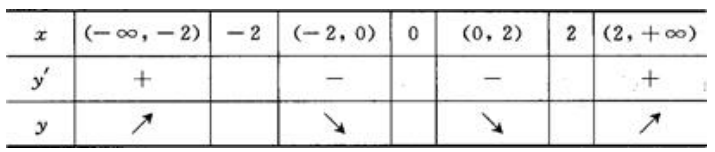 所以单调减少区间为(-2,0)和(0,2).
所以单调减少区间为(-2,0)和(0,2).
主观题
1、当 .
.
答 案:证:设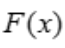 =ex-x-1,
=ex-x-1,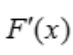 =ex-1.当x<0时,
=ex-1.当x<0时,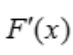 <0,F(x)单调递减,所以当x<0时,F(x)>F(0)=0,即ex-x-1>0,得ex>1+x.
<0,F(x)单调递减,所以当x<0时,F(x)>F(0)=0,即ex-x-1>0,得ex>1+x.
2、证明:当x>1时,x>1+lnx.
答 案:证:设f(x)=x-1-lnx,则f'(x)= .当x>1时,f'(x)>0,则f(x)单调上升.所以当x>1时,f(x)>f(1)=0,即x-1-lnx>0,得x>1+lnx.
.当x>1时,f'(x)>0,则f(x)单调上升.所以当x>1时,f(x)>f(1)=0,即x-1-lnx>0,得x>1+lnx.
填空题
1、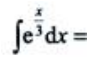 ().
().
答 案: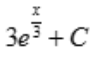
解 析: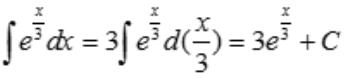 .
.
2、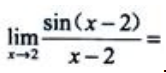 ().
().
答 案:1
解 析:由等价无穷小可知,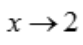 时,即
时,即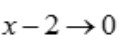 ,
,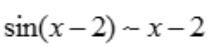 ,故
,故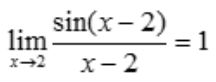 .
.
简答题
1、设函数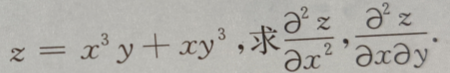
答 案: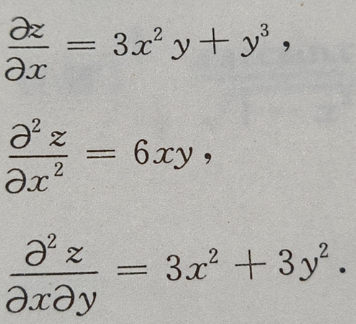
2、求函数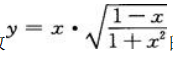 的倒数。
的倒数。
答 案:等式两边同时取对数得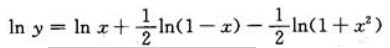 方程两边同时对x求导有
方程两边同时对x求导有 故
故
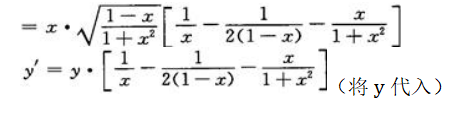
精彩评论